Involute of a Circle Engineering Drawing

Anfractuous toothing is often used in mechanical engineering science for gears, as it offers favorable meshing and is piece of cake to produce.

• 1 Introduction
• 2 Construction of an involute
• 3 Nomenclature
• 4 Tooth size: the module
• v Gear size: the standard reference pitch diameter
• half dozen Diametral pitch
• vii Tooth shape: the pressure bending
• 8 Base pitch

Introduction

In mechanical technology, the involute is used nearly exclusively as a tooth grade for gears. Such gears are called involute gears. The use of involute toothing is due on the 1 paw to the favorable meshing (engagement of 2 gearwheels). On the other paw, involute gears can be manufactured toll-effectively due to the relatively simple tool geometry.

Figure: Involute gears

Construction of an involute

In the case of involute toothing, the shape of the molar flanks consists of two involutes of circles (called involutes for short). An involute is constructed past rolling a and so-called rolling line around a base of operations circle. The resulting trajectory bend describes the shape of the anfractuous. 2 mirror-inverted involutes then class the bones shape of a tooth.

Figure: Constructing an anfractuous past rolling a straight line on a circumvolve

Animation: Amalgam an involute past rolling a straight line on a circumvolve

The involute can also exist constructed past unwinding a string from a circle. The string is ever kept taut during unwinding. The cease of the string then also describes the shape of the involute.

Figure: Constructing an involute by unwinding a string on a circle

Animation: Amalgam an involute by unwinding a string on a circle

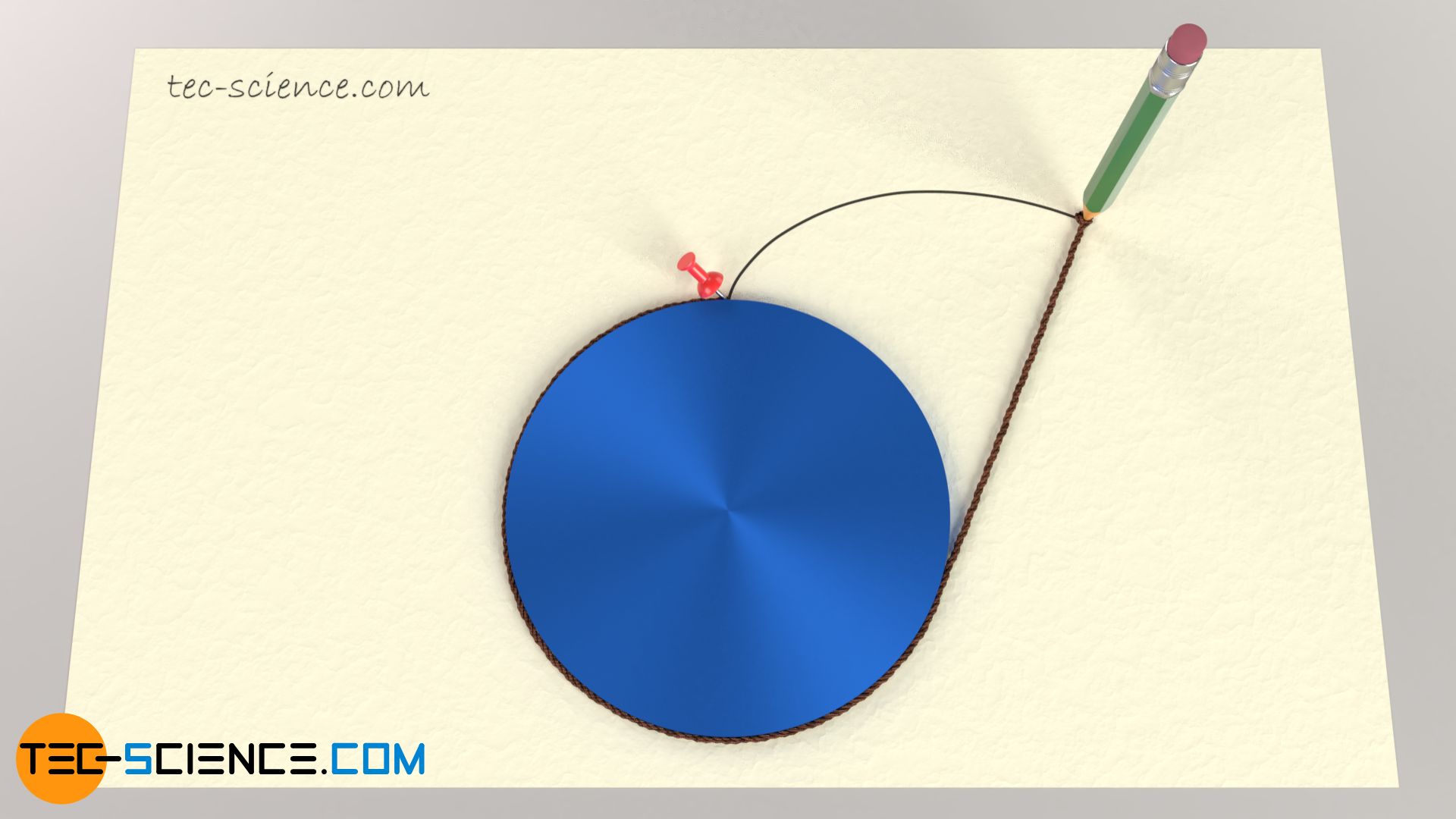
An involute is constructed by unwinding a rolling line on a base of operations circle or by unwinding a string from the base circle!

The longer the involute, the greater the curvature radius, i.e. the smaller the curvature of the involute. From the structure of the involute information technology becomes clear that the radius of curvature corresponds exactly to the arc length on the base of operations circle.

Figure: Curvature radius of the involute at a small altitude from the base circle

The longer the involute, the less curvature it has!

Yet, the flank shape cannot only be influenced by changing the base circumvolve bore. By means of a so-called profile shift, the tooth flanks of gearwheels are composed of the more afar function of the involute, while the base circumvolve bore remains the aforementioned. The tooth flank is therefore less curved and "flatter". During meshing with another gear, the contact forces can thus exist distributed more evenly. This reduces the tooth load and thus the tooth wear.

Contour shifted gears use the less curved part of the involute for the tooth shape!

Nomenclature

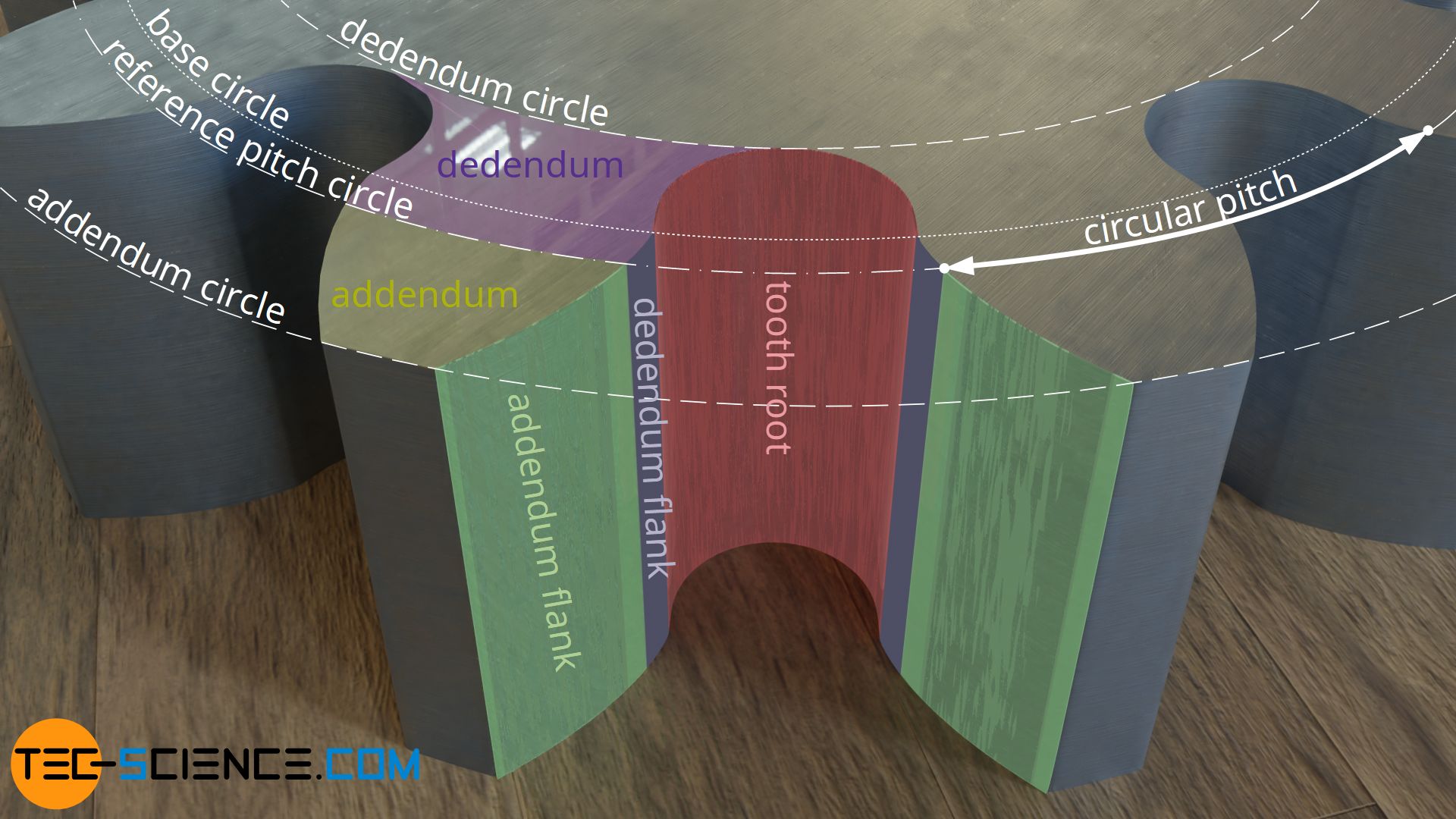
In order to avoid contact between the tip and the root of the tooth of two meshing gears, the root of the molar is rounded out (chosen fillet). The resulting bore at the root of the molar is called the root bore (dedendum circle). Analogous to the root diameter, a tip diameter can be assigned to the tip of the gear (addendum circumvolve).

Figure: Base circumvolve, addendum circumvolve and dedendum circle of an involute gear

Note, that at that place is no contact between the tooth flanks of two meshing gears inside the base of operations circle! For further information run into article meshing.

There is no contact of the tooth flanks within the base circle!

Figure: Nomenclature of an involute gear

The size of a gearwheel is defined by the so-called standard reference pitch diameter. Strongly simplified, this bore corresponds to the diameters of imaginary cylinders that roll on each other. The tooth spacing is related to this bore and is referred to every bit the circumferential pitch or circular pitch. The circular pitch is the arc altitude between two tooth flanks of the same direction on the pitch circumvolve. This circular pitch must be identical for all gears so that the teeth can mesh without interfering.

The spacing of the teeth can basically as well be related to the base circle. In this case, the pitch is then referred to as the base pitch. More detailed information on this can be institute in the next section.

Tooth size: the module

In order to characterize gears and above all to ensure that the teeth of ii gears can mesh properly, one of the most important parameters is the then-called module m. The module is a mensurate of the molar size of a gear and is commonly given in millimeters (if the unit is in inches, the module is also chosen "English Module".). Only if the teeth of gears are of the same size and thus accept the same module can they be paired with each other!

Effigy: Geometry of an involute gear

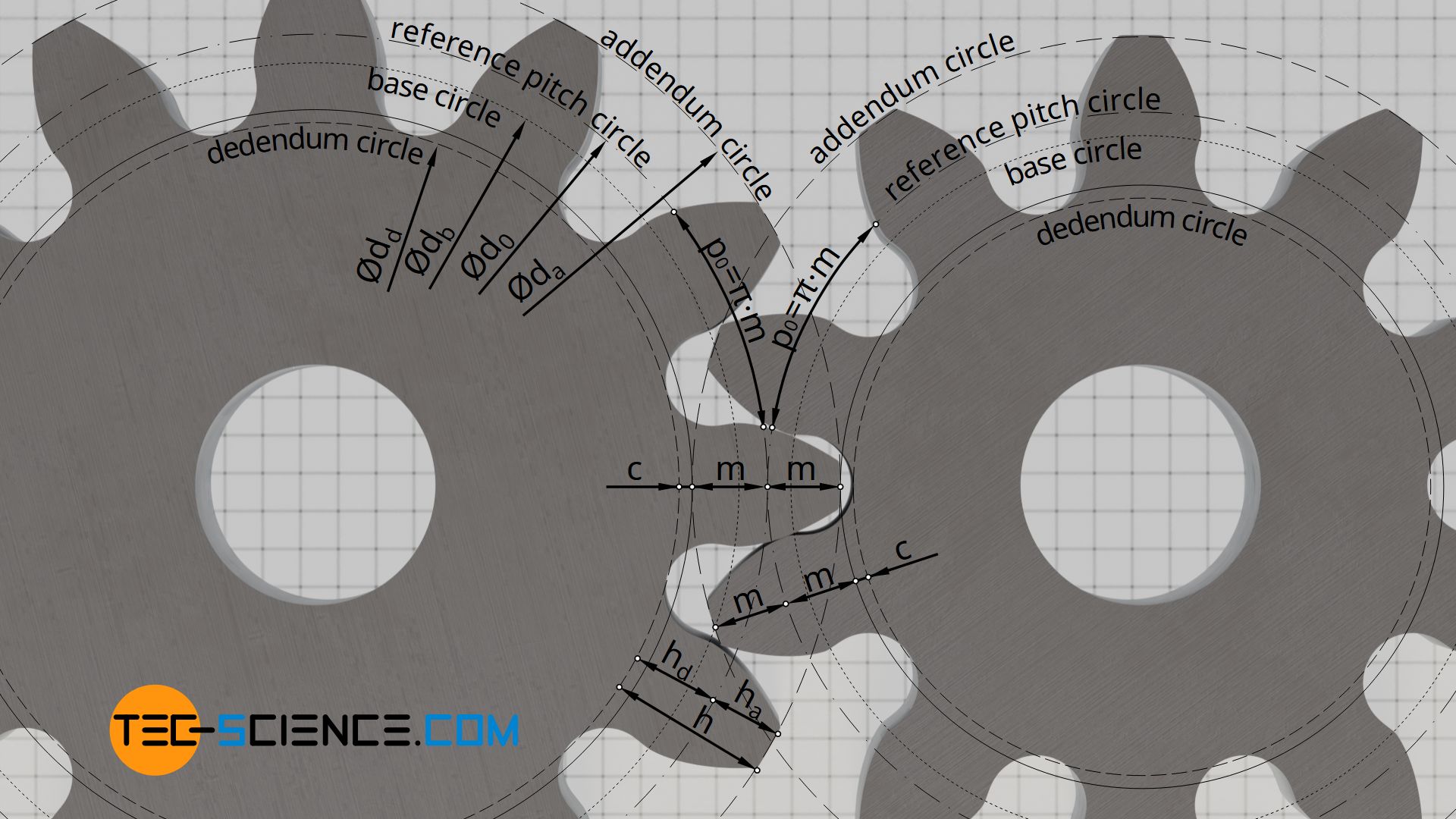
The module corresponds directly to the addendum h_a. The dedendum h_d also results from the module, whereby a clearance c is as well taken into account. The clearance corresponds to the amount by which the tooth root is additionally deepened to avoid contact between the tip and root of two gearwheels. Depending on the application, the clearance is typically x% to xxx% of the module (often 0.167⋅m). The whole depth of the tooth h thus results from twice the value of the module m, plus the clearance c.

\begin{align}
&\boxed{h_a = m} ~~~\text{annex} \\[5px]
&\boxed{h_d = m + c} ~~~\text{dedendum} \\[5px]
&\boxed{c = 0,167 \cdot g} ~~~\text{clearance } \\[5px]
&\boxed{h = h_a + h_d = 2 \cdot k + c} ~~~\text{whole depth} \\[5px]
\end{align}

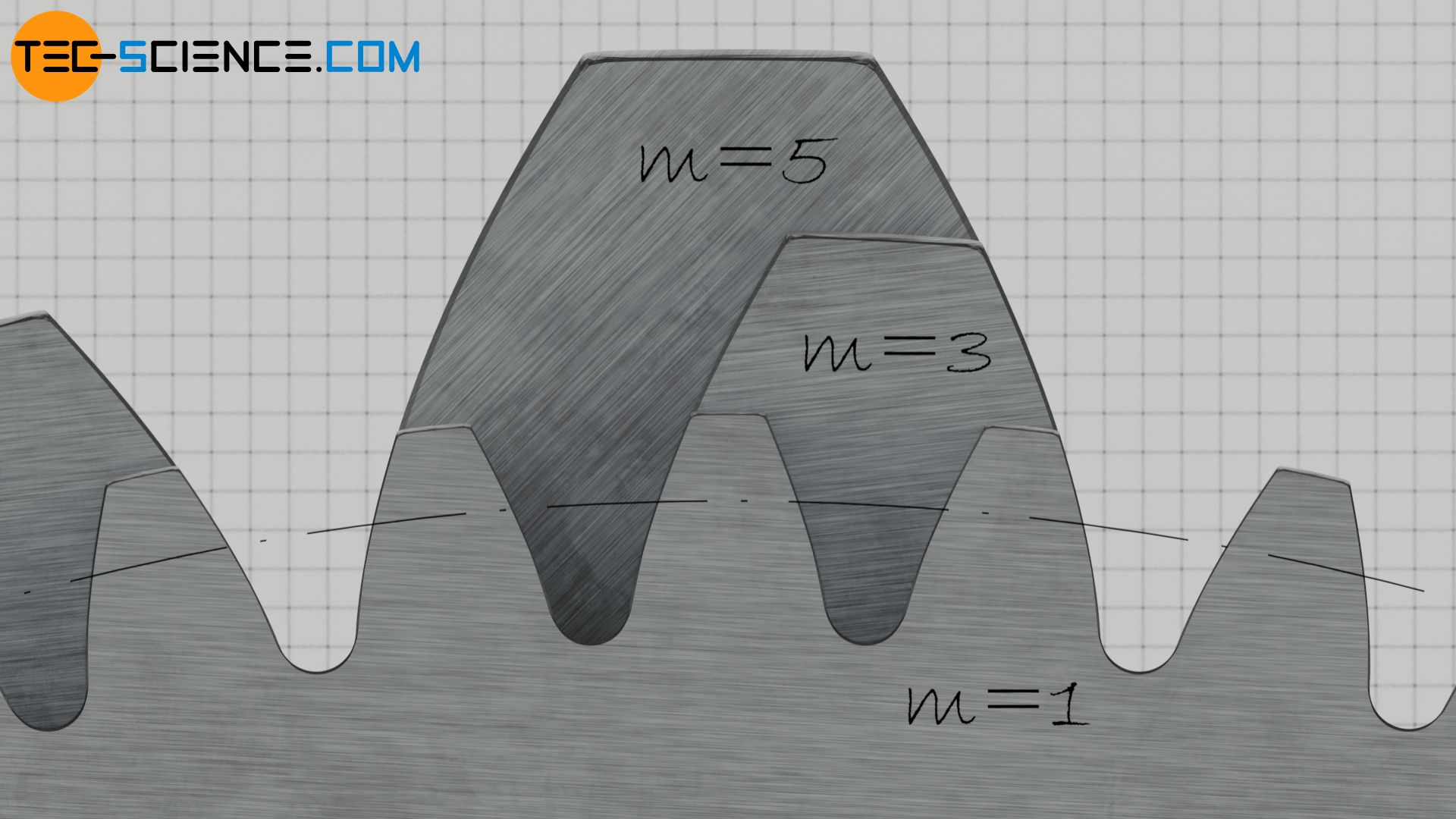
The module is a mensurate of the tooth size: the larger the module, the larger the tooth! Only gears with the same module tin exist paired!

The figure below shows three gears of the same size (i.eastward. identical reference pitch circles), simply manufactured with unlike modules. The next section deals with the reference pitch circle in more detail.

Figure: Influence of the module on the tooth size

Effigy: Comparison of unlike modules

Gear size: the standard reference pitch diameter

If the clearance is neglected for now, the molar is "divided" past the standard reference pitch diameter at half depth, so to speak. The standard reference pitch diameter d₀ results from the product of module thousand and number of teeth z and is a mensurate for the size of the gear:

\begin{align}
&\boxed{d_0 = m \cdot z} ~~~\text{standard reference pitch bore} \\[5px]
\end{align}

Note that, in contrast to the and then-called operating pitch diameter, the reference pitch diameter is a fixed size of a gearwheel which is determined solely by the product of the module and the number of teeth.

The standard reference pitch diameter serves only as a reference circle for specifying the circular pitch p₀, i.e. the tooth spacing which must be identical for all gears if they are to mesh. This arc length p₀ between two identical tooth flanks tin be adamant from the quotient of the pitch circle circumference u₀=π⋅d₀ and the number of teeth z:

\brainstorm{align}
&p_0 = \frac{u_0}{z} = \frac{\pi \cdot d_0}{z} = \frac{\pi \cdot m \cdot z}{z} = one thousand \cdot \pi \\[5px]
&\boxed{p_0 = thousand \cdot \pi} ~~~\text{round pitch} \\[5px]
\cease{marshal}

At this point it becomes over again articulate that only gears with identical modules can be paired with each other, because obviously only then the tooth spacing p₀ for all gears are identical and the teeth can mesh properly.

The standard reference pitch diameter is a measure for the size of a gearwheel. The circular pitch of the teeth is related to this diameter. All gears to be paired must have identical circular pitches on their standard reference pitch circles and thus identical modules!

The standard reference pitch diameter d₀ tin at present be used to decide the tip diameter d_a (addendum circumvolve) and the root diameter d_d (dedendum circle):

\brainstorm{marshal}
&d_a =d_0 + 2 \cdot h_a = m \cdot z + 2 \cdot one thousand   \\[5px]
&\boxed{d_a =m \cdot (z+2)}  ~~~\text{tip diameter (annex circle bore)} \\[5px]
&d_d = d_0 – 2 \cdot h_d = m \cdot z – 2 \cdot (m+c)   \\[5px]
&\boxed{d_d = k \cdot (z-2) – 2 \cdot c}  ~~~\text{root diameter (dedendum circle bore)} \\[5px]
\end{marshal}

For gears that are not contour-shifted, the round tooth thickness south₀ and the tooth space width eastward₀ on the reference pitch circle are identical in length and thus represent to one-half the circular pitch p₀. Two gears can thus be paired without backlash. Thus no "rattling" occurs during the change of the management of rotation.

\brainstorm{align}
&\boxed{s_0 = e_0 = \frac{p_0}{2} = \frac{m}{2} \cdot \pi} ~~~\text{circular tooth thickness , tooth space width} \\[5px]
\finish{align}

Figure: Standard center altitude

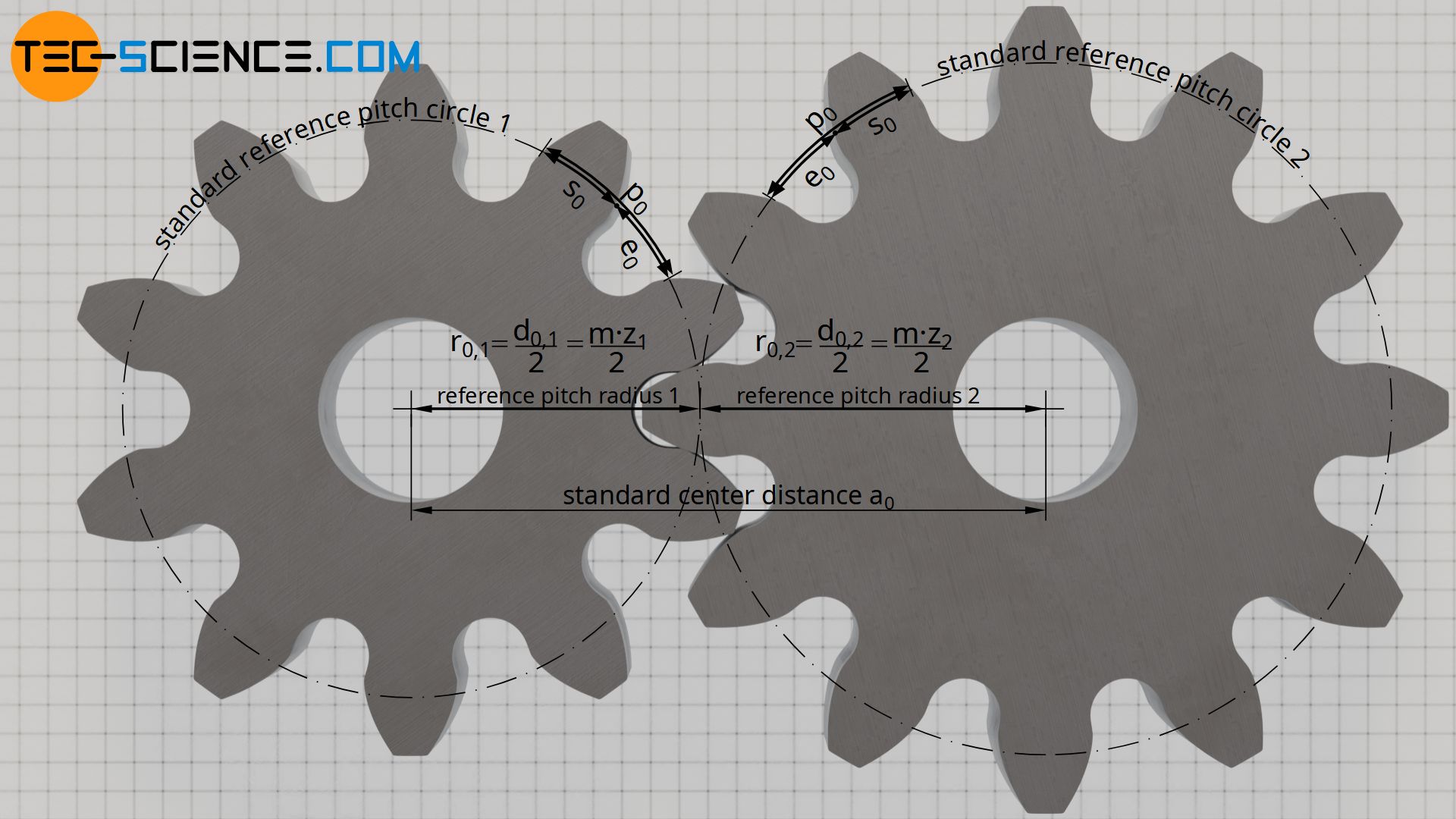
The center distance of the 2 non-profile shifted gears for backfire-free pairing is referred to equally the standard center distance a₀. The standard heart distance results from the sum of the two reference pitch radii or half the sum of the reference pitch diameters:

\begin{marshal}
&\boxed{a_0 = \frac{d_{0,1}+ d_{0,ii} }{2} = \frac{m}{ii} \cdot (z_1+z_2)} ~~~\text{standard heart distance} \\[5px]
\end{align}

Diametral pitch

Instead of the module, the so-calleddiametral pitch is often used as a measure of the tooth size. The diametral pitch DP corresponds to the changed of the module m:

\begin{align}
&\boxed{DP = \frac{1}{m} = \frac{z}{d_0} } ~~~\text{diametral pitch} \\[5px]
\end{align}

Therefore, the diametral pitch indicates how many teeth per unit of measurement length of pitch diameter a gearwheel has.

Author's note: The term diametral pitch ist somewhat a lilliputian bit confusing, since in dissimilarity to the terms base of operations pitch oder circular pitch, the diametral pitch doesn't land a "distance per molar", but just the contrary: "tooth per distance". To be consistent, the module chiliad should therefore be the "real diametral pitch". This inconsistence is the reason why I'thou non using the term diametral pitch any farther, but only the module.

Tooth shape: the force per unit area angle

If the teeth of gears are to mesh perfectly, non merely the molar sizes must lucifer (described by the module g), just likewise the tooth flank shape must match. This flank shape is described by the then-chosen pressure bending. The pressure level angle is described in more detail in this department.

The shape of the involute and thus the tooth flank is only dependent on the base circle bore. Each base circle therefore e'er has a specific involute. All involutes are geometrically similar, i.due east. they can be "scaled" (enlarged or reduced in size) to the same shape.

The flank shape of a gear is determined by the base circle diameter, whereby all involutes of whatever base circles are geometrically similar to each other!

If larger base circle diameters are used to construct the tooth flanks for a sure gear size (i.e. for identical pitch diameters), the teeth will tend to await "foursquare". With smaller base diameters, however, the tip of the teeth tend to look "pointed". The figure below shows the tooth shapes for different base diameters with identical reference pitch circles. The tooth size, i.due east. the module, was chosen the same for all gears!

Figure: Flank shape for dissimilar base circle diameters

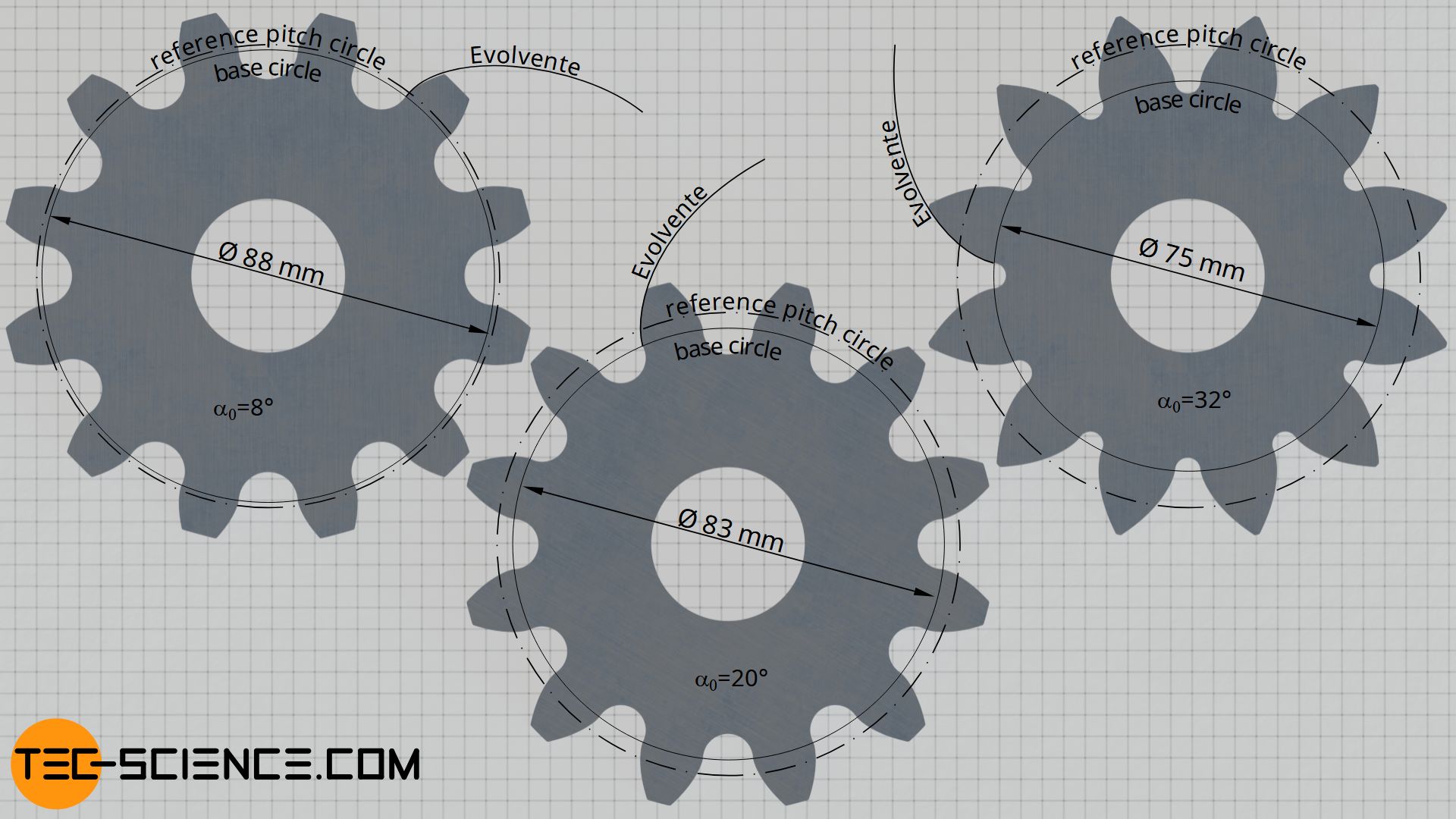
Two gears can only mesh properly if they have the same tooth shape. This is only the case if the ratio of base circle diameter to reference pitch bore is identical for all gears. When increasing the number of teeth and thus the reference pitch diameter, the base circle diameter must increase by the same corporeality so that the molar shape remains identical (this corresponds to the "scaling" of the involutes mentioned above).

In addition to the module, a further parameter must therefore exist defined which describes the ratio of the base of operations circle diameter to the reference pitch diameter and thus the tooth shape. The relationship between the base of operations circle and the pitch circle becomes apparent when two gears with no profile shift are paired without backlash. In this example, the center altitude corresponds to the standard heart distance a₀ and the pitch circles of both gears touch on each other at the so-chosen pitch point C.

Effigy: Connection between base of operations circle and pitch circle (pressure angle)

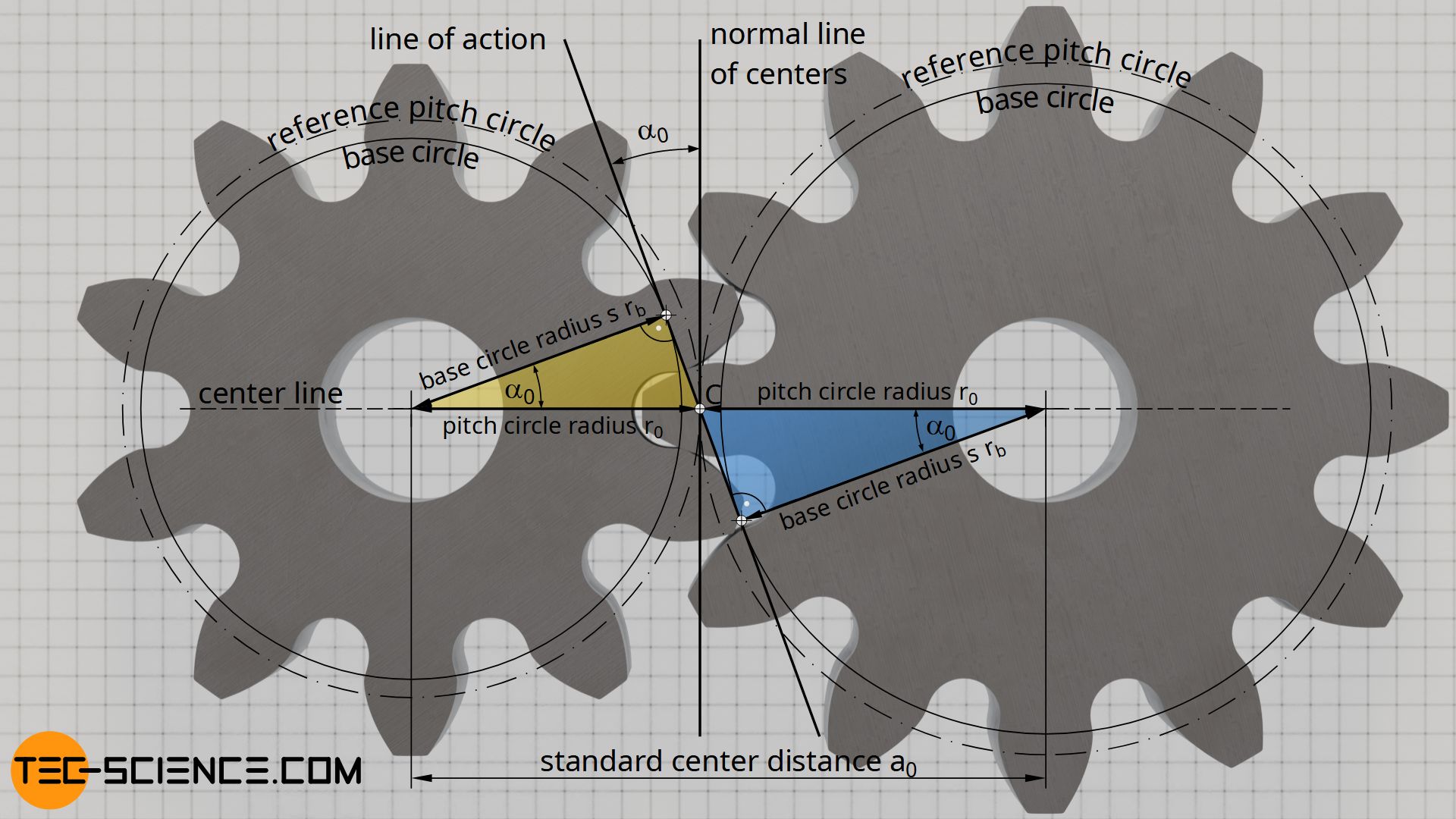
If a tangent is now applied to the two base circles of the gears, this so-called line of action encloses a certain angle with the normal of the center line. This bending is chosen the pressure angle α₀. Equally the yellow and blue triangles in the figure above testify, the base circle radii r_b and the pitch circle radii r₀ are related by this force per unit area angle α₀:

\begin{align}
&\cos(\alpha_0) = \frac{r_b}{r_0}  \\[5px]
&\boxed{\cos(\alpha_0) = \frac{d_b}{d_0}} ~~~\alpha_0 \text{ : pressure angle} \\[5px]
\end{marshal}

In practice, the bore ratio of the base circle to the pitch circle, and thus the flank shape, is determined by this pressure angle. Contained of the module, a pressure level angle of α₀ = twenty° is normally used for all gears. However, there are likewise gears with pressure angles of 14.5° or 25°.

In the figure "Flank shape for different base circle diameters", a pressure bending of viii° was selected for the left gear and an angle of 20° for the center gear and an bending of 32° for the right gear.

The fact that the pressure angle directly determines the flank shape of a gear is also immediately obvious from an manufacturing point of view. In general, gears are manufactured by gear hobbing. In this instance, the flank shape of the gear is determined by the inclination of the cutting edges of the rack-shaped tool profile. This tool angle corresponds directly to the pressure angle α₀!

Note:
– the module is a measure for the molar size!
– The standard reference pitch bore is a measure out for the gear size!
– The pressure level angle is a measure for the shape of the tooth flank!

Base of operations pitch

All involutes of a gear are equidistant to each other, i.eastward. the right-angled distances of ii adjacent involutes are identical for all points on an anfractuous. This correct-angled distance also corresponds to the arc section on the base circumvolve, since the involutes are constructed by rolling a rolling line on the base of operations circle without sliding. This curved distance of the involutes on the base of operations circle (= curved distance of the molar flanks!) is therefore too called base pitchp_b.

Figure: Involute as equidistant lines (base pitch)

The base pitch p_b on the base of operations circle is not to be confused with the circular pitchp₀ on the pitch circle.However, both pitches are not independent of each other. Just as the base circle diameter and the reference pitch diameter are proportional to each other by the pressure bending α₀ (run into previous section), the same ratio likewise applies to the corresponding pitches on the base circumvolve and the pitch circle:

\brainstorm{align}
&\boxed{\cos(\alpha_0) = \frac{p_b}{p_0}} \\[5px]
\end{align}

Effigy: Deviation between round pitch and base pitch

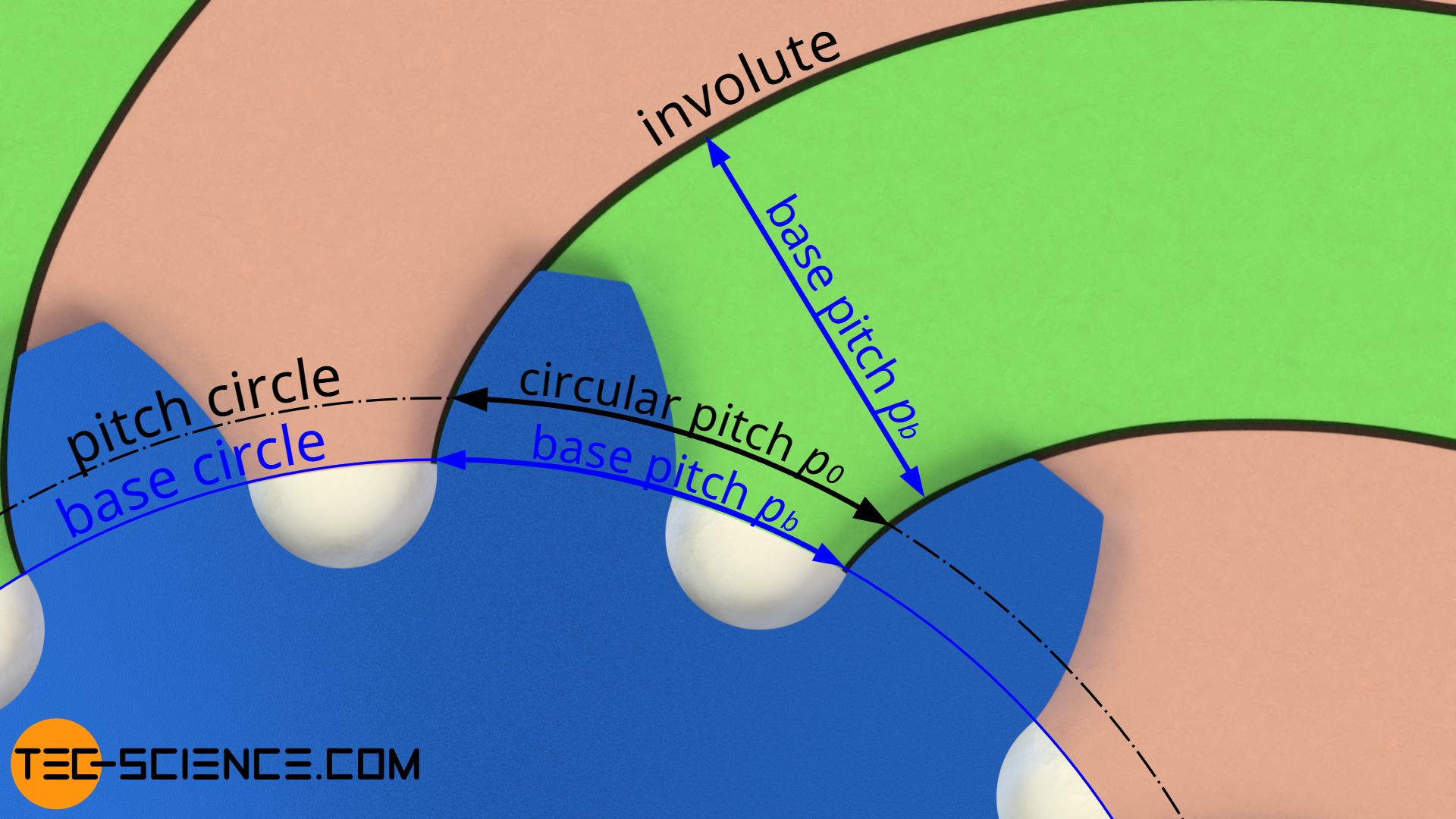
The rectangular distance between two involutes (i.e. the base of operations pitch!) as well corresponds to the distance betwixt two tooth flanks touching each other during meshing ("meshing pitch")!

Figure: Difference between round pitch and base pitch

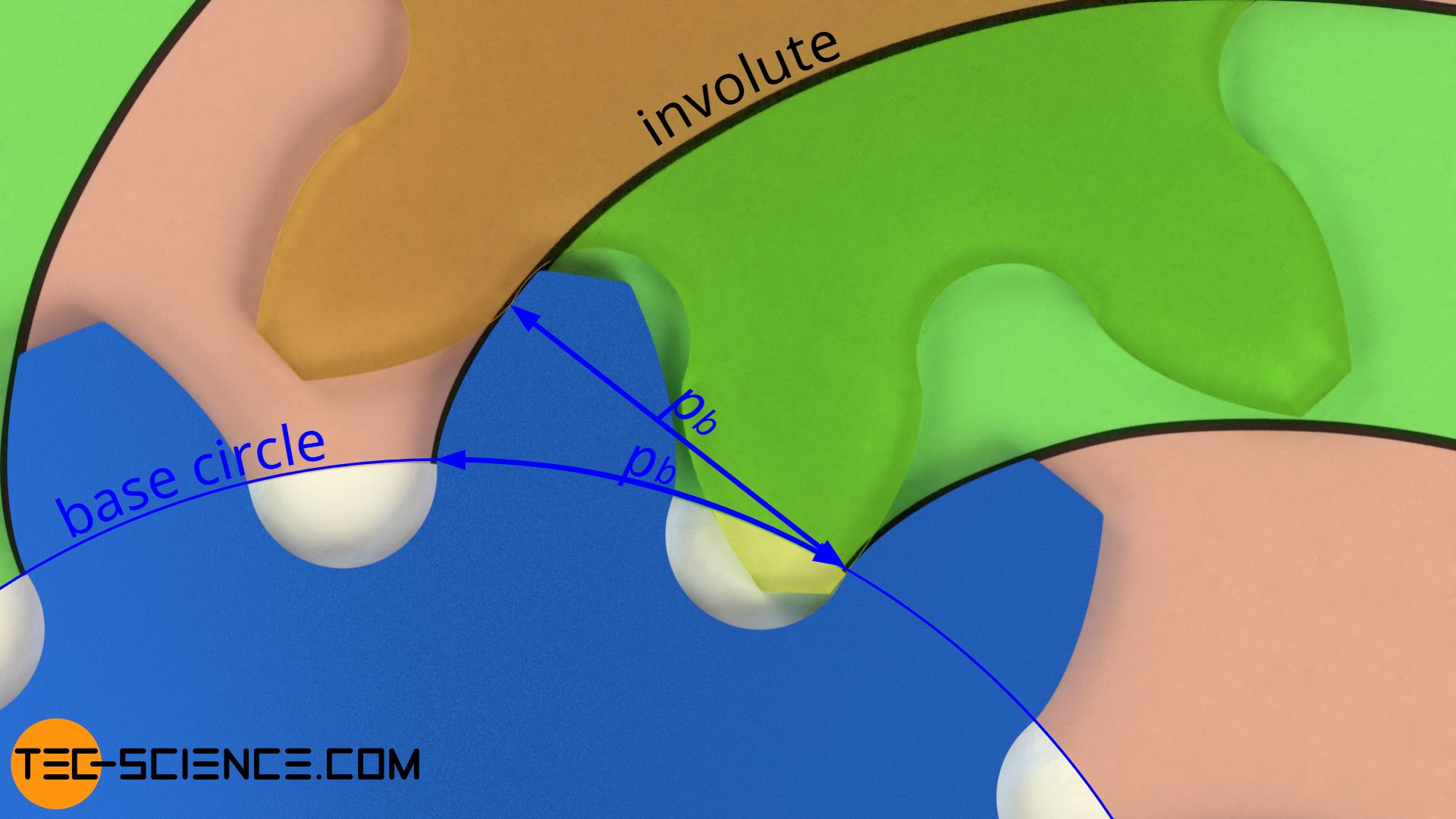
The base pitch corresponds to the distance between two meshing flanks and results from the correct-angled distance between ii side by side involutes ("meshing pitch")!

More information on the engagement of 2 anfractuous gears tin can be found in the article Meshing of anfractuous gears.

hollandconfort.blogspot.com

Source: https://www.tec-science.com/mechanical-power-transmission/involute-gear/geometry-of-involute-gears/

Share this post